
Menu

Compound interest is a type of interest in which the interest amount is added to the principal amount on a regular basis, and new interest is accrued over previous periods’ interest. It is a simple calculation related to personal savings plan or strategy, as well as long-term growth of a stock portfolio, and it is a highly strong tool for raising your capital.
Our compound interest calculator is a handy tool that can help you:
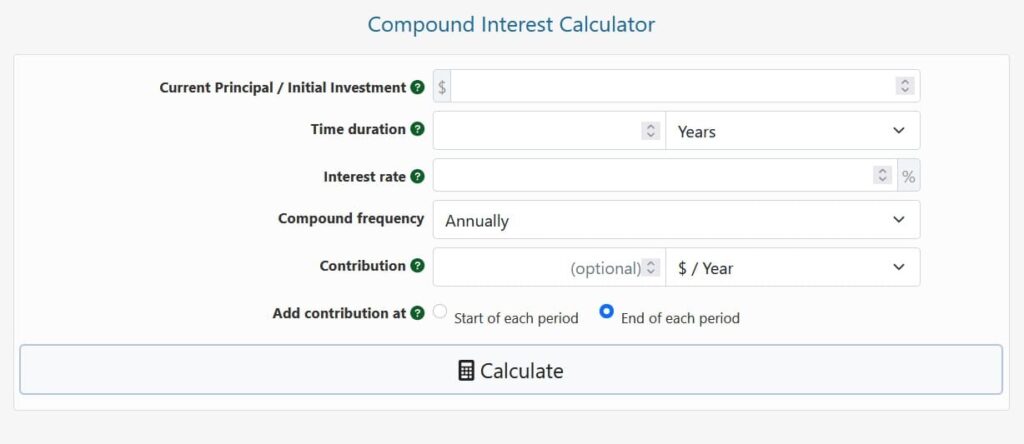
Begin by entering your initial deposit or investment, or, if you already have a deposit, your current balance. This is the starting point for all calculations. Then specify how long you wish to hold the deposit or investment, which is commonly expressed in years, but other time periods are also supported. Enter the annual interest rate (APR), which does not take compounding into account and is commonly shown as APR on offers and bank product comparison sites. Because the compounding period affects the Annual Percentage Yield (APY), also known as the Effective Annual Interest Rate, which our calculator calculates for you, this is not the same as the APY.
The value of your deposit or investment at the conclusion of the term, the interest accrued, the effective interest rate, the total amount of further deposits made, and the percentage capital growth will all be calculated by the interest calculator.
The compound interest formula is:
A=P.(1+r/n)n.t
where A is the Accrued amount (principal plus interest), P is the principal, r is the Annual interest rate (not compounded, not APY) in decimal, t is the time in years, and n is the number of compounding periods per unit t.
The formula for the effective interest rate is:
I=[(A/P)1/t -1].100
The effective interest rate is I, and the remainder of the notation is the same as before. These formulas can be twisted to solve for principal and time as needed. These formulas can help you figure out how to compute compound interest.
The compounding frequency, or how often interest is added to the principal, can have a little beneficial impact on the effective interest rate compared to the nominal yearly interest rate. Using our compound interest calculator with shorter compounding periods can quickly show you how large that influence is. Daily compounding (also known as continuous compounding) produces the most effective rate, whereas monthly or yearly compounding produces somewhat lower results.
The goal of this exercise is to calculate the accumulated interest, total accrued interest, and capital growth percentage for a certificate of deposit with an initial value of $10,000 and an annual interest rate of 2% during a three-year period. To make the computation easier, no contributions (monthly or yearly deposits) will be made.
During the first year, the math is limited to simple interest calculations. Starting with $10,000 at 2% interest, $10,000 x 0.02 = $200 in interest results in a total of $10,200 at the conclusion of year one. The interest rate is just the rate of capital growth. In year two, we begin compounding by adding the $200 in interest to the principal, giving us a total of $10,200 in year two. The interest on that is now $10,200 x 0.02 = $204, rather than $200 as in year one, therefore the deposit will be worth $10,404 at the end of year two. The capital growth rate can be calculated using a simple percentage increase formula: $10,404 / $10,000 = 4.04 %.
The table below shows the result of applying these equations to years 3, 4, and 5, and the final result:

After 5 years, the total value is $11,041, but it would have been only $11,000 with simple interest. This may not appear to be a significant amount, but if the rate of return is higher or the compounding period is longer, the compounding effect can be significant.
The difference between simple and compound interest has already been demonstrated in the preceding example. Let’s look at a hypothetical investment with a 15% yearly rate of return over 10 years to emphasise the point. Note how the difference grows as the number of compounding periods increases, assuming the returns can be reinvested at the same rate at the end of each year.

On the same $10,000 starting investment, the difference in return is more than $2,500 after five years and more than $15,000 after ten years. That’s a capital growth of 405% compared to just 250%. Compounding’s power is demonstrated in this example.
© 2021 All rights reserved
Ask Your Query